Biblioteca Estática Gráfica
En primer lugar se presentan ejemplos de estática gráfica sencillos para análisis de diagramas de forma impuestos.
A continuación, se recopilan dos ejemplos particulares utilizando la
metodología de la parábola para el análisis y resolución de geometrías en forma de arcos.
En primer lugar, se muestra el análisis completo de una estructura a compresión pura
compuesta por dos arcos.
En segundo lugar se muestra Free-Form Thruses, dónde se compara el comportamiento
de un forma cualquiera con su funicular impuesta, para poder definir barras articuladas
que compensen el momento flector.
Metodlogía estática gráfica
Puente Peatonal 1
El esquema principal viene definido por las siguiente condiciones:
- El puente, de 12 metros de longitud, tiene un peso F1 que se trasmite a un cable N1 en el centro de la plataforma.
- N1, N2 y N3 son los tirantes que sujetan el puente, y son sometidos a análisis para resolver los esfuerzos asociados a cada elemento.
- La Figura (a) muestra una configuración del diagrama de forma del puente en la plataforma Geogebra, donde los puntos A y B son extremos móviles los cuáles el usuario puede modificar para obtener diferentes combinaciones para ver su correspondiente diagrama de Fuerza.
Puente Peatonal 2
El esquema principal viene definido por las siguiente condiciones:
- F1 y F2 representan los puntos de apoyo de los tirantes sobre el puente. Dichos puntos son interactivos y se mueven a lo largo de la luz del puente.
- N1, N2 y N3 son los tirantes que sujetan el puente, y son sometidos a análisis para resolver los esfuerzos asociados a cada elemento.
- Diagrama de Forma interactivo véase Figura (a), dónde los puntos A y B son extremos móviles a lo largo de sus contornos dónde el usuario puede ver las diferentes combinaciones que forman en el espacio para ver su correspondiente Diagrama de Fuerza.
Como se muestra en la Figura (b), se establecen dos diagramas de forma:
- Diagrama de fuerza en morado, cuyas condiciones en cargas estarían en equilibrio con el diagrama de forma final..
- Diagrama de fuerza discontinuo en rojo, asociado al diagrama de forma impuesto por el usuario, dónde Nip son los segmentos paralelos asociados a a los tirantes del diagrama de forma.
El diagrama de fuerza en rojo no permanece en equilibrio ya que el punto A no pertenece al segmento N3p.
Para encontrar la funicular que permanezca en equilibrio con la imposición de cargas, el usuario debe modificar las cotas de los apoyos.
Como se puede apreciar en la anterior Figura (a), la altura de A ha aumentado con respecto a la posición en la primera Figura (a) y con ello, se ha configurado un nuevo diagrama de Fuerza, coincidiendo con la solución de equilibrio.
Con respecto al diagrama de fuerza (Figura(b)), las longitudes de los diferentes segmentos en centímetros (N1,N2 y N3) representan los esfuerzos a los que estarían sometidos los diferentes elementos del diagrama de forma.
Metodología de la parábola
Arcos consecutivos
- Se establecen 3 apoyos (Nodo 1, Nodo 2 y Nodo 3). Dichos nodos serán paramétri- cos, pudiendo resolver la geometría para diferente luz total.
- Se define dos grupos de cargas:
- Cargas12, asociado al número total de cargas distribuidas a lo largo de la Luz12.
- Cargas23, asociado al número total de cargas distribuidas a lo largo de la Luz23.
- Dichas cargas discretizan la luz entre los diferentes apoyos.
- Para cada par de apoyos ij, se establecen los puntos paramétricos Gij, hacen referencia al ángulo que definirá la reacción total en los apoyos.
- Para cada par de apoyos ij, se establecen los puntos Iij, hacen alusión a la altura máxima de la funicular resultante, y viene definida por la mitad del segmento Gij - Pij
- Los segmento Aij y Bij para cada par de nodos, los cuáles se utilizan para resolver la funicular final.
A continuación se muestra la metodología para resolver el problema, definido con las siguiente características:
Ya que los apoyos no permanecen en la misma cota, se necesita realizar un método iterativo. En primer lugar, se establece un Polo aleatorio, con el fin de generar dos funiculares cualquiera, que cumplan únicamente las condiciones de contorno en carga.
Construyendo las funiculares a través de dichos diagramas de forma, los apoyos 1’, 2’ y 3’ no reflejan ninguna relación con los apoyos originales, se extraen los segmento aij y bij para cada par de apoyos, los cuáles definen la geometría de la funicular aleatoria por los puntos Nodoi′ , Nodoj′ y I′ ij.
Dichas paralelas tienen sus homólogas en las condiciones de contorno iniciales (segmentos Aij y Bij para cada par de apoyos), se utilizan como paralelas en las intersecciones Ibi y Iia, y las intersecciones entre ambas rectas definen el Polos Finales.
Con la información de los diagramas de fuerza que componen los Polos finales, se construye los arcos que satisfacen la condición de contener los apoyos 1, 2 y 3.
Las funiculares presentadas en Figura (a) y (b) vienen caracterizadas por la anterior imposición de variables.
De cara a resaltar las conclusiones más importantes del diagrama de fuerza:
- Las condiciones de contorno en carga total viene dado por el vector WTotal.
- Los vectores R1, R2 y R3 hacen referencia tanto a la reacción en kN que habría en sus nodos correspondientes para establecer el equilibrio estático, como el ángulo paralelo para formar el polígono funicular de forma en los extremos del arco.
¡Ejemplo Interactivo!
Ha llegado el momento, comprueba la teoría por tí mismo y prueba diferentes combinaciones!
Free Form Thruses
El segundo ejemplo trata sobre el diseño controlado de estructuras con una forma no funicular y de forma libre.
Dichas estructuras pueden transformarse en funiculares de forma libre añadiendo un sistema de rigidez a tensión en relación a la magnitud del momento de flexión en la curva.
Las acciones de esta estructura libre de forma reforzada será las mismas que las de la solución funicular (línea discontinua).
En este ejemplo, la forma general de la estructura libre de forma está controlada por una curva de control en 3 puntos interiores (C, D y E) y dos exteriores asociados a los apoyos de la estructura (A y B).
Dado un conjunto de cargas (en este caso, una carga uniforme a lo largo de la curva de control), se puede construir una solución funicular a través de los soportes y un tercer punto elegido.
Esta línea representa una posible solución sin flexión para la carga dada. El momento de flexión M en cualquier punto a lo largo de la curva de control es proporcional a su desviación de la solución funicular: M = Hv, donde H es el empuje (horizontal) de la estructura, y v es la distancia vertical entre la curva de control y la funicular.
Donde la solución funicular y la curva de control se intersectan, el momento de flexión es cero. Al elegir la magnitud de la fuerza de tensión en el cable de refuerzo, T, se determina completamente la forma del sistema de refuerzo, ya que M = Td, donde d es la distancia perpendicular a la curva de control. Este sistema transforma la curva de control en una línea de empuje con la forma libre deseada.
En un entorno interactivo, se pueden explorar y diseñar con precisión diferentes configuraciones de este sistema estructural complejo sin realizar cálculos, simplemente determinando la forma general de la estructura utilizando los puntos de control de la curva de control, eligiendo la forma de la funicular a través de la ubicación del punto de flexión cero y eligiendo el tamaño deseado de la fuerza del cable en el sistema de refuerzo.
Para comenzar el análisis de la metodología es necesario establecer una serie de condiciones:
- Se define una curva que tiene cinco puntos de control (A, B, C, D y E), la cuál viene limitada por los puntos A y B (apoyos de la estructura).
- Se divide la luz de la estructura en NCargas + 1, haciendo referencia a la carga distribuida que actúa en la funicular.
- Se define el punto F, pertenece a la curva generada, y se utiliza para establecer de forma paramétrica funiculares que contengan dicho punto.
A continuación se muestra la metodología para resolver el problema, definido con las siguiente características:
Para comenzar, se establecen las paralelas RMitadAF y RMitadFB que permiten delimitar la mitad entre los puntos AF y FB.Acontinuación, se trazan las rectas ParalelaAF y ParalelaFB e intersectan con las paralelas anteriores en R1 y R2.
Con todo ello, se ha creado el diagrama de fuerza asociado a la funicular que pasa por el punto F. Como se ve en la siguiente Figura, se han puesto en dirección Y las 12 cargas de 0,7 kN, por la escala utilizada (Escala 1kN :1 cm), el vector RTotal equivale a 8,4 centímetros.
El punto U hace referencia al porcentaje de carga que admite cada funicular en relación a la posición del punto F a lo largo del eje X.
Una vez establecido dichos puntos, se trazan paralelas con A1, A2, B1 y B2 cómo se muestra en la Figura anterior, y se construye el diagrama de fuerza Trial.
Para encontrar el Polo que defina la funicular final, utilizamos el PoloT1 y PoloT2 y establecemos paralelas A2 y B2 respectivamente, la intersección define el PoloF.
La longitud de los vectores ATotal y BTotal hacen referencia a la reacción en los apoyos A y B, tanto en dirección como en sentido. La escala que relaciona la longitud con la fuerza, se ha definido como 1 centímetro es un 1 kN.
Se unen los puntos que representan las cargas al PoloF y construimos la funicular en el diagrama de forma, dónde el punto RF es la intersección de las paralelas ATotal y BTotal por sus apoyos respectivamente.
Como se ha comentado anteriormente, la funicular es una posible solución sin flexión, para trasladar la misma definición a la curva de control es necesario aplicarle un momento proporcional a la desviación con respecto a la funicular establecida.
Viene dado por la siguiente expresión:
Donde H refleja el empuje horizontal de la estructura, v la distancia vertical entre el punto de la funicular y la curva de control, T es la tensión del cable kN, y d longitud de la barra que genera dicha transformación.
Se establece la variable T como paramétrica, donde el usuario puede combinar diferentes magnitudes para resolver el valor d y visualizar su influencia en la estructura final.
Cabe destacar que cuándo el punto de la curva de control tiene mayor cota que el punto de la funicular, se establece la barra que genere el momento contrario.
¡Ejemplo Interactivo!
Ha llegado el momento, comprueba la teoría por tí mismo y prueba diferentes combinaciones!
Biblioteca TNA
A continuación se muestra el índice de los ejemplos realizados en función de sus características principales:
| Descripción | Metodología | Puntos interiores | Puntos exteriores |
|---|---|---|---|
| Primera Cúpula | Formulación Lineal | 1 | 4 |
| Segunda Cúpula | Formulación Lineal | 4 | 4 |
| Tercera Cúpula | Formulación Lineal | 8 | 8 |
| Great Court | Implementación Matricial | 16 | 48 |
| Striatus Bridge | Implementación Matricial | 56 | 25 |
Formulación Lineal
Primera Cúpula
La primera cúpula propuesta presenta una planta rectangular de 2x2 metros discretizada en 5 puntos con un total de 4 secciones. Al ser una planta sencilla, se puede emplear el análisis simple.
Condiciones de contorno
- Se establecen como apoyos los nodos 2 ,3 ,4 y 5, haciendo referencia que su cota será cero, y por lo tanto su altura es conocida.
- Se establece una carga (P) parametrizable controlada por el usuario, cabe destacar que su magnitud será en Newtons.
- Se establece un factor de escala (ζ) parametrizable controlada por el usuario.
Una vez establecida la Malla Primal Γ, se plantea el equilibrio vertical en función de la numeración establecida.
Se reformula en el plano horizontal a través de la geometría de la planta para tener como incógnita la altura de los puntos internos, en este caso sólo uno, en vez de las fuerzas, es decir, la geometría pasa a ser el objetivo de resolución del problema.
¡Ejemplo Interactivo 1!
Ha llegado el momento, comprueba la teoría por tí mismo y prueba diferentes combinaciones!
Segunda Cúpula
La segunda cúpula propuesta presenta una planta rectangular de 10x10 metros discretizada en 8 puntos con un total de 5 secciones.
Condiciones de contorno
- Se establecen como apoyos los nodos 5 ,6, 7 y 8, haciendo referencia que su cota será cero, y por lo tanto su altura es conocida.
- Se establece una carga (P) parametrizable controlada por el usuario, cabe destacar que su magnitud será en Newtons.
- Se establece un factor de escala (ζ) parametrizable controlada por el usuario.
Una vez establecida la Malla Primal Γ, se plantea el equilibrio vertical en función de la numeración establecida.
Las longitudes de las ramas ji en la Malla Primal Γ están definidas mediante LHji, véase Figura 2.4.
¡Ejemplo Interactivo 2!
Ha llegado el momento, comprueba la teoría por tí mismo y prueba diferentes combinaciones!
Tercera Cúpula
La tercera cúpula propuesta presenta una planta cuadrada de 8,4x8,4 metros discretizada en 16 puntos con un total de 11 secciones. Al ser una planta sencilla, nuevamente, se puede emplear el análisis simple.
Condiciones de contorno
- Se establecen como apoyos los nodos 9, 10, 11, 12, 13, 14, 15 y 16, haciendo referencia que su cota será cero, y por lo tanto su altura es conocida.
- Se establece una carga (P) parametrizable controlada por el usuario, cabe destacar que su magnitud será en Newtons.
- Se establece un factor de escala (ζ) parametrizable controlada por el usuario.
Una vez establecida la Malla Primal Γ, se plantea el equilibrio vertical en función de la numeración establecida.
¡Ejemplo Interactivo 3!
Ha llegado el momento, comprueba la teoría por tí mismo y prueba diferentes combinaciones!
Implementación Matricial
A continuación, se muestran los dos ejemplos realizados a través de la implementación matricial!
Great Court
La primera propuesta como ejemplo realizado mediante la resolución matricial es el de la cubierta acristalada del Great Court en el British Museum de Londres, un área rectangular de 73 x 97 metros que contiene una circunferencia de 44 métros de diámetro desplazada con un offset de 3 metros en el eje x que representa la “sala de lectura” o Reading Room. Los datos geométricos se han obtenido de un estudio sobre el desarrollo de la cúpula de J.K.Williams (2001).
Condiciones de contorno
- Se establecen como apoyos los nodos 1, 2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 y 16, haciendo referencia que su cota será cero, y por lo tanto su altura es conocida.
- Consta de una malla discretizada en 48 nodos, dónde hay 48 ramas y está formada por 32 polígonos.
- Se establece una carga (P) parametrizable controlada por el usuario, cabe destacar que su magnitud será en Newtons.
- Se establece un factor de escala (ζ) parametrizable controlada por el usuario.
Una vez definida la caracterización global de la Malla Primal Γ, se dispone a realizar
la matriz C de relaciones nodales.
Cómo se ha explicado en la teoría, el procedimiento consiste en seguir el
flujo de fuerzas propuesto, y completar la matriz con 1 si el punto representa la cabeza
de la línea de fuerza, -1 si representa la cola de la línea de fuerza, ó 0 en el resto
de los casos.
El siguiente paso es el desarrollo de la Malla dual a partir de las ramas convergentes
en cada punto orientadas en el sentido de las agujas del reloj las entrantes al nodo y
en el opuesto las salientes.
Este proceso ha tenido una dificultad añadida para su realización debido a que las
ramas son muy irregulares y los ángulos complejos, pero finalmente se ha llegado a
una malla como la mostrada en la Figura 4.8, dónde Pi hace referencia al polígono que representa el equilibrio nodal del punto i en la Malla Primal Γ
A partir de esta malla se puede construir la matriz de relaciones del diagrama recíproco C* de dimensiones m x p siendo m el número de líneas de fuerza y p el número de polígonos de la malla original, que en la dual se han convertido en puntos.
Tal y cómo se ha definido en la programación, se ha definido como valores paramétricos tanto la carga asociada a cada nodo interior que será uniforme para todos como el factor de escala ζ, dando la oportunidad al usuario de componer diferentes soluciones de estructuras.
Una vez realizado lo anterior, se calculan las longitudes de las ramas en ambos diagramas y se aplican la ecuación para la resolución del problema y poder definir las alturas de los nodos interiores.
¡Ejemplo Interactivo 4!
Ha llegado el momento, comprueba la teoría por tí mismo y prueba diferentes combinaciones!
Striatus Bridge
La segunda propuesta como ejemplo realizado mediante la resolución matricial es el Puente Striatus, realizado gracias tanto al grupo de investigación Block Research Group cómo a la firma británica de arquitectura Zaha Hadid Architects.
La Malla Primal Γ se compone de la siguiente información:
Realizamos su diagrama recíproco mediante la herramienta RhinoVAULT estableciendo la escala a centímetros.
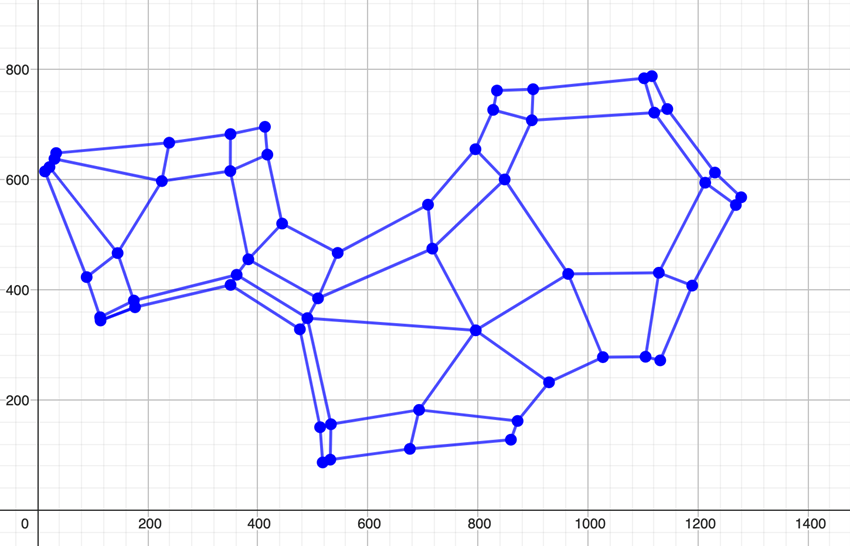
Por último, se muestra el comportamiento de la estructura en la plataforma Geogebra en función de los parámetros principales cómo el peso y el factor de escala!
Para más información sobre el modelo visita el siguiente enlace de Archivo de Puente Striatus TNA.