La Estática Gráfica es una rama de la ingeniería mecánica que se encarga del estudio de cuerpos en equilibrio. Se basa en la aplicación de las leyes físicas y matemáticas para determinar las fuerzas que actúan en un sistema y asegurar que este se encuentre en equilibrio.

Para dicho método se utiliza dos diagramas geométricos que son dependientes, llamados los diagramas de Forma que representan la geometría de la estructura, y los diagramas de Fuerza que hacen referencia al equilibrio interno y externo de las fuerza, véase Figura (a).

Para este caso en particular se parte de una geometría dada, dos barras unidas sometidas a una carga puntual y biapoyadas en sus extremos opuestos.

Para representar el equilibrio, se obtiene el polígono del diagrama de Fuerza, y los esfuerzos se representan como flechas que se colocan sobre una estructura en dos dimensiones, véase Figura (b). Estas flechas representan la dirección y magnitud de los esfuerzos asociados a la estructura.

Cabe destacar que la relación fundamental entre ambos diagramas queda definida por una imposición de escalas, la primera en referencia a la escala entre el modelo real y el modelo del dibujo, y la segunda con respecto a la escala entre la equivalencia de fuerzas y su longitud en el dibujo.

Como se ve en la Figura (a), el nodo C se representa en el diagrama de fuerza a través de un polígono cerrado, donde la carga puntual se coloca verticalmente, y tanto en el inicio como en el final de dicho segmento se trazan las paralelas del diagrama de forma asociadas a N1 y N2.

La intersección de ambas paralelas en el diagrama de fuerza se denomina Polo, véase Figura (b), y delimita la magnitud de los esfuerzos asociados a los elementos del diagrama de forma.

Dicha metodología se utiliza para un primer diseño de la forma, incluyendo la construcción de puentes, edificios, máquinas y otros tipos de estructuras.

Introducción

Thrust Network Analysis ofrece un enfoque visual para encontrar formas de estructuras funiculares en tres dimensiones. El método resuelve el equilibrio estático de redes funiculares de manera sencilla utilizando la geometría, lo que permite seguir intuitivamente y comprender completamente el proceso de diseño estructural.

Metodología

1. Construcción de la malla Primal Γ

En primer lugar es necesario definir la cuadrícula que va a determinar los patrones de esfuerzos. Las ramas representan las posibles rutas de distribución de cargas a través de la estructura, y los nodos están asociados a las posiciones de los centroides dónde actuaría la carga propia de la estructura.

2. Definición de las cargas nodales

Debido a que se establece un diagrama discretizado, las cargas son aplicadas en los puntos que componen la malla. Aunque la carga principal es el peso propio, las cargas que se van a imponer en los ejemplos son arbitrarias ya que no se ha definido ningún material determinado para obtener una solución general para una carga seleccionada por el usuario.

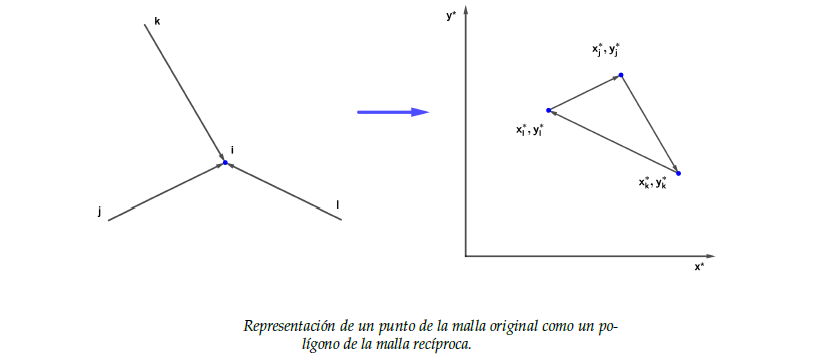
3. Generación de la malla Dual Γ*

La malla Dual Γ* es consecuencia directa de la definición geometría de la mala Primal Γ mediante la definición de figuras recíprocas de Maxwell, en dónde enuncia "las ramas correspondientes permanecen paralelas y el equilibrio nodal en la retícula Primal está garantizado por polígonos cerrados en la retícula Dual". Es importante comentar que la mala Dual tiene una escala desconocida ζ, ya que la relación entre la malla Primal y la Dual independiente de sus escalas relativas.

4. Generación de la malla Dual Γ*

Usando los datos en geometría, asociados a la malla Primal y la malla Dual, junto a las condiciones de contorno como los pesos aplicados en los nodos y los apoyos dentro de la malla Primal, el problema se puede resolver usando una optimización lineal de un solo paso, definiendo la escala ζ mencionada anteriormente.

Formulación lineal

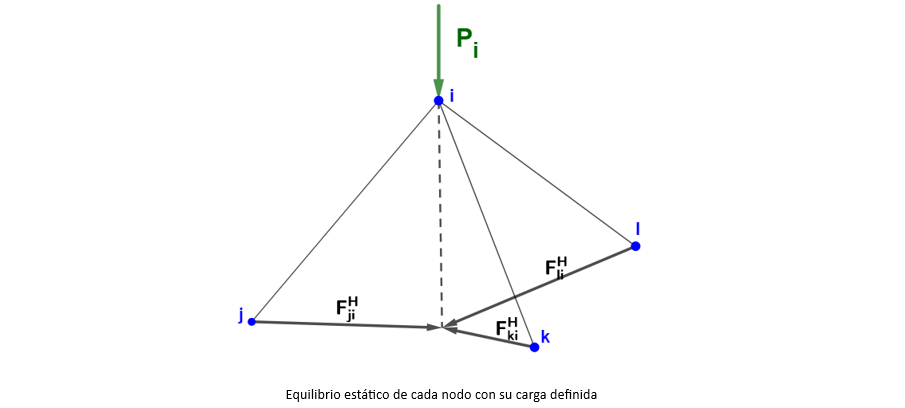
La formulación se inicia planteando el equilibrio estático en cada uno de los no- dos, de tal manera que el sumatorio de las componentes verticales de las fuerzas compense la acción vertical.
Dado que esto es aplicado en cada punto, habrá tantas ecuaciones como nudos internos tenga la estructura ya que los puntos de contorno o apoyos ya están determinados haciendo referencia a que su altura está definida en el plano XY con z=0.

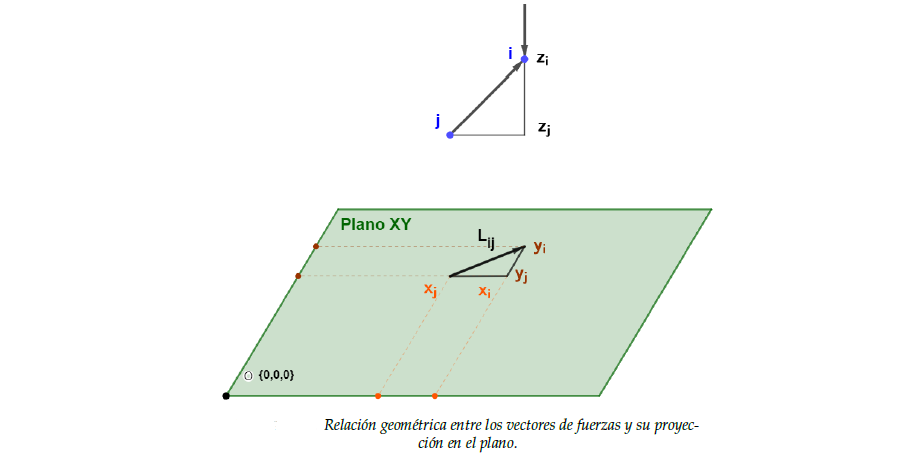
Describimos la Ecuación 2.1 en función de componentes en fuerzas, utilizando la proporcionalidad geométrica.

En consecuencia de lo anterior, la Ecuación 2.2 queda en función de las fuerzas horizontales, la longitud de las ramas de la malla primal y las alturas de los nodos.

La magnitud de las fuerzas horizontales se relaciona a través de la longitud de la representación de las fuerzas en la malla dual, por eso la ecuación puede expresarse en términos de la geometría de la malla propuesta, que cumple las condiciones de equilibrio y compresión pura, y del factor de escala para controlar la geometría de la solución final.

Reordenando la Ecuación 2.2 y sustituyendo la relación de las fuerzas en función de sus respectivas longitudes en las diferentes mallas como en la Ecuación 2.3, dónde r hace referencia a la inversa del valor de la escala desconocida de la malla Dual, ζ:

La relación entre las longitudes de ambas mallas se puede agrupar en un término llamado Cn (dónde el subíndice n hace referencia al nodo de la malla Primal) ya que todos los parámetros son conocidos. Con las condiciones de contorno impuestas y el factor de escala seleccionado por el usuario, sólo queda determinar la altura de los puntos.

El procedimiento presentado es aplicable a mallas Primales con un número de nodos reducido, ya que se adapta a la capacidad de codificación.
Sin embargo, cuando la estructura se compone de un grado mayor a nivel de discretización, existe otro procedimiento para resolver ese sistema de ecuaciones más voluminoso, a continuación se presenta dicho análisis computacional.

Implementación Matricial

Basándose en los mismos principios, la implantación computacional se sirve de vectores y matrices que representan no sólo la geometría de ambas mallas como en el caso anterior, sino también la conectividad de las ramas de los diferentes diagramas.
Para ello se establece una convención para la enumeración de los nodos, dónde en primer lugar se numeran los nodos interiores, haciendo referencia a los nodos con cargas aplicadas, para a continuación enumerar los nodos exteriores, haciendo referencia a los nodos que formarán parte de los apoyos de la estructura.
De esta forma, los vectores coordenada x , y , z (n x 1) seguirán el orden de coordenadas de nodos interiores (n_i x 1) y coordenadas de nodo exteriores (n_b x 1.).

La matriz C (dimensiones n x nº Ramas), será la encargada de relacionar la conectividad de los nudos.
Cabe mencionar que aunque haya flechas salientes del nudo, que podrían interpretarse como fuerzas de tensión, solo implican una propuesta de camino del flujo de las cargas, no indica la dirección de las fuerzas en los nodos.
Como se muestra en la Figura 2.6, las flechas se orientan para asegurar el estado de compresión pura, dónde el convenio de vectores implica que las entrantes tienen el sentido de las agujas del reloj y las salientes siguen el giro antihorario.

Para establecer la matriz C, se sigue el siguiente convenio para cada nodo en la malla Primal:

Para el caso visto en la Figura 2.6, su matriz C estará definida con las dimensiones (9x12) y su conectividad vendrá dada por la siguiente configuración:

La matriz C tiene su homóloga dual C* y también se empleará en la aplicación del método. Igual que la primera, representa las relaciones entre los puntos de la malla dual teniendo en cuenta que los polígonos de la malla primal han pasado a ser puntos de la recíproca, y los puntos de la original son polígonos en la dual.

Una vez establecidas las coordenadas de ambas mallas Primal y Dual, juntos a las matrices C y C* se pueden obtener los vectores de coordenadas de las ramas de ambos diagramas y calcular las longitudes para obtener un sistema análogo al que se empleaba en el caso de aplicación a un único punto.
Las matrices U, U*, V y V* son los vectores de coordenadas diagonalizados.

De la teoría de Schek [1974] para la formulación de la ecuación de equilibrio y aplicando el concepto de densidad de fuerza de Linkwitz y Schek [1971] se obtiene el sistema final para la resolución del problema en función del factor de escala. El vector P representa las cargas verticales aplicadas en cada nodo y tiene dimensiones n_i x 1.

Separando la ecuación en nudos internos y externos y agrupando los términos conocidos se obtiene una formulación similar a la del apartado anterior.

La matriz D_i tiene dimensiones n x n_i y D_btiene dimensiones de n x n _b.

Despejando el vector de alturas de la ecuación el sistema a implementar queda como:

Con este tipo de metodología, podemos abordar estructuras de un mayor grado de discretización como se muestra en la siguiente Figura.